静电场及其应用
电荷
摩擦过的琥珀具有电荷，自然界的电荷只有两种，被称为正电荷与负电荷。
电荷的多少叫做电荷量，用 $Q$ 或 $q$ 表示，它是一个标量，正/负号对应正与负电荷。国际单位制中，它的单位是库仑，符号是 $C$ ，$1C$ 定义为 $1A$ 电流在 $1s$ 内传送的电荷量。
众所周知，原子由质子（+）、中子（不带电）、电子（-）组成，其中离原子核较远的电子容易受到外界的作用脱离原子，摩擦起电就指当两种物质组成的物体互相摩擦时，一些受束缚较弱的电子会转移到另一个物体上。
金属中原子的外层电子往往会脱离原子核的束缚而在金属中自由运动，这种电子叫作自由电子。失去自由电子的原子便成为带正电的离子，它们在金属内部排列起来，每个正离子都在自己的平衡位置附近振动而不移动，只有自由电子穿梭其中，这就是金属导电的原因，而绝缘体中几乎不存在能自由移动的电荷。
注意：摩擦起电时，丢失的不是自由电子，这也解释了绝缘体也可以摩擦起电。
当一个带电体靠近导体时，由于电荷间相互吸引或排斥，导体中的自由电荷便会趋向或远离带电体，使导体靠近带电体的一端带异种电荷，远离带电体的一端带同种电荷。这种现象叫作静电感应。
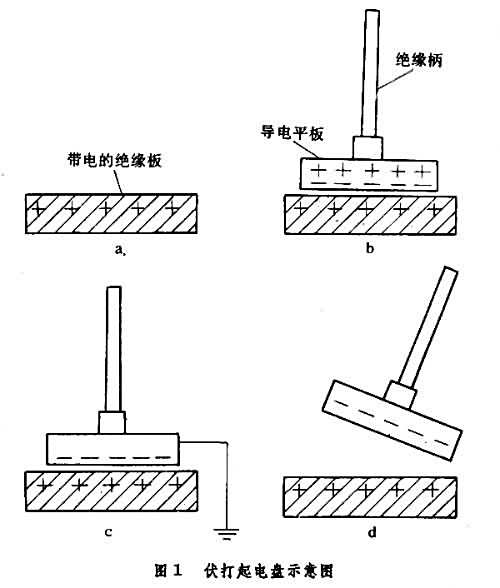
下图b，不带电的平板通过静电感应使得正电荷聚集于远端（即上方），通过图c的接地，大地变成远端，正电荷来到大地（本质上是大地给予了更多电子），分离后即带电。
这是个对比表格
| 特性 | 摩擦起电 (Charging by Friction) | 接触带电 (Charging by Conduction/Contact) | 感应起电 (Charging by Induction) |
|---|---|---|---|
| 基本原理 | 不同材料摩擦时，电子因对原子核束缚力的差异而从一个物体转移到另一个物体。 | 带电体与不带电导体直接接触，电荷在两者之间重新分布或转移。 | 带电体靠近不带电导体（不接触），通过电荷的重新分布（静电感应）使导体带电，通常需要接地。 |
| 接触要求 | 需要两个物体之间直接摩擦接触。 | 需要带电体与不带电体直接接触。 | 不需要带电体与不带电体直接接触，只需靠近。 |
| 电荷转移 | 有电子从一个物体转移到另一个物体，导致两者都带电。 | 有电荷（通常是自由电子）从带电体转移到不带电体，或从不带电体转移到带电体。 | 无带电体本身的电荷转移。电荷在不带电导体内部重新分布，或通过接地与大地发生转移。 |
| 最终带电性质 | 两个物体带上等量异种电荷。例如，丝绸摩擦玻璃棒，玻璃棒带正电，丝绸带负电。 | 不带电物体带上与原带电体相同的电荷。 | 不带电物体带上与原带电体相反的电荷。 |
| 原带电体的电量 | 摩擦后两物体总电量守恒，原电中性物体的总电量不变。 | 原带电体的电量会减少，因为它将一部分电荷转移给了另一个物体。 | 原带电体的电量基本不变（或几乎没有损失），因为没有电荷从它上面转移走。 |
| 适用物体类型 | 较适用于绝缘体（电荷不易移动，容易在摩擦区域积累）。 | 主要适用于导体（电荷可以自由移动）。 | 主要适用于导体（内部有自由电荷可以重新分布），绝缘体也能发生感应，但电荷不能自由移动。 |
| 持久性 | 产生的电荷通常可以持续一段时间，特别是在干燥环境下。 | 产生的电荷相对持久，直到物体接地或电荷耗散。 | 产生的感应电荷在带电体移开后可能消失（如果没有接地），但通过接地可以使物体永久带电。 |
| 例子 | 用梳子梳头时头发会“飘”起来；脱毛衣时发出“噼啪”声；气球摩擦头发后可以吸附在墙上。 | 用带电的金属棒接触一个不带电的金属球，金属球也会带上与金属棒相同的电荷。 | 伏打起电盘的工作原理；带电云层导致地面感应出异种电荷（雷电现象）。 |
一个与外界没有电荷交换的系统，电荷的代数和保持不变。这就是电荷守恒定律。
元电荷指电子所带电荷量，是 $e=1.60 \times 10^{-19}$
库仑定律
类似于质点，我们有形状、大小、电荷分布情况忽略不计的点电荷。
类似于万有引力定律，注意到电荷之间也有作用力，我们有库仑定律，其中k被称为静电力常量，q是两个电荷的电荷量。F是静电力，或称库仑力。
$$
F=k\frac{q_1 q_2}{r^2}\\
其中 k=9.0 \times 10^9 N \cdot m^2 / C^2
$$
注意：此公式仅适用于真空中的两静止电荷
电场&电场强度
电荷的周围存在电场，处在电场中的其他电荷受到的作用力就是这个电场给予的。例如，电荷A对电荷B的作用力，就是电荷A的电场对电荷B的作用。静止电荷所产生的场被称为静电场。
由于电场在电荷的相互作用中表现出其性质，故为研究电场，我们引入试探电荷，它的体积&电荷量都特别小，我们认为它不影响原来的电场。与试探电荷对应，场源电荷或源电荷指电场中原有的电荷。
我们希望用试探电荷所受静电力反映电场的特征。注意到对于电场的同一点，静电力随试探电荷的电荷量改变，但是它们之比不变，我们定义电场强度 $E$ 为
$$
E=\frac{F}{q}
$$
电场强度取决于场源电荷和位置，而与此位置上的电荷无关。
$E$ 是个矢量，方向同正电荷在此处受静电力的方向。
在某一点的电场强度等于它所在的所有电场强度之矢量和。
通过推导库仑定律，我们得到点电荷作为场源电荷时的电场强度：
$$
F=k\frac{q}{r^2}
$$
通过微元法（即将球形分割成无数块）可以证明，它同样适用于一个球形带电体，$r$为球心到该点距离。
电场线是画在电场中的一条条有方向的曲线，曲线上每点的切线方向表示该点的电场强度方向，每一点的电场强度则由此处的电场线疏密程度反映。
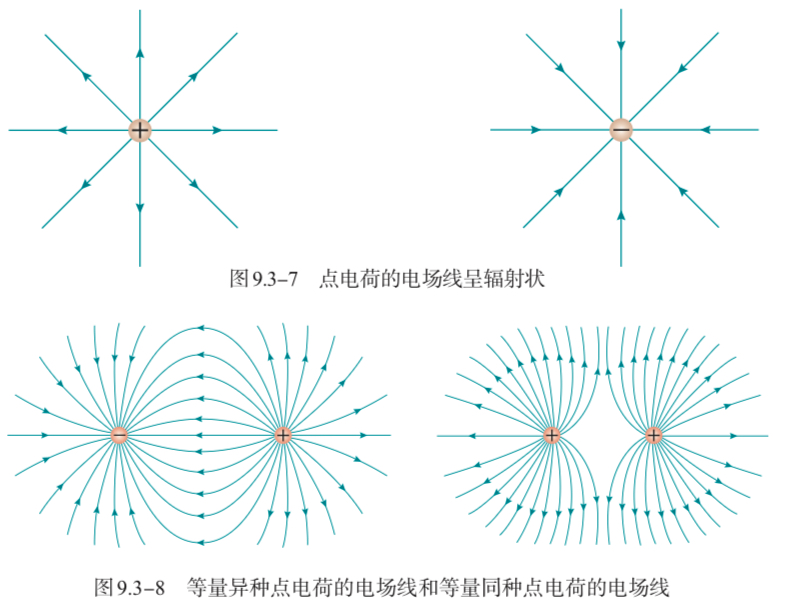
上图是一些常见的电场线。对于等量异种电电荷，在两电荷连线上，电场强度最小，对于同种点电荷呢…趋势相同！下面有desmos为证：
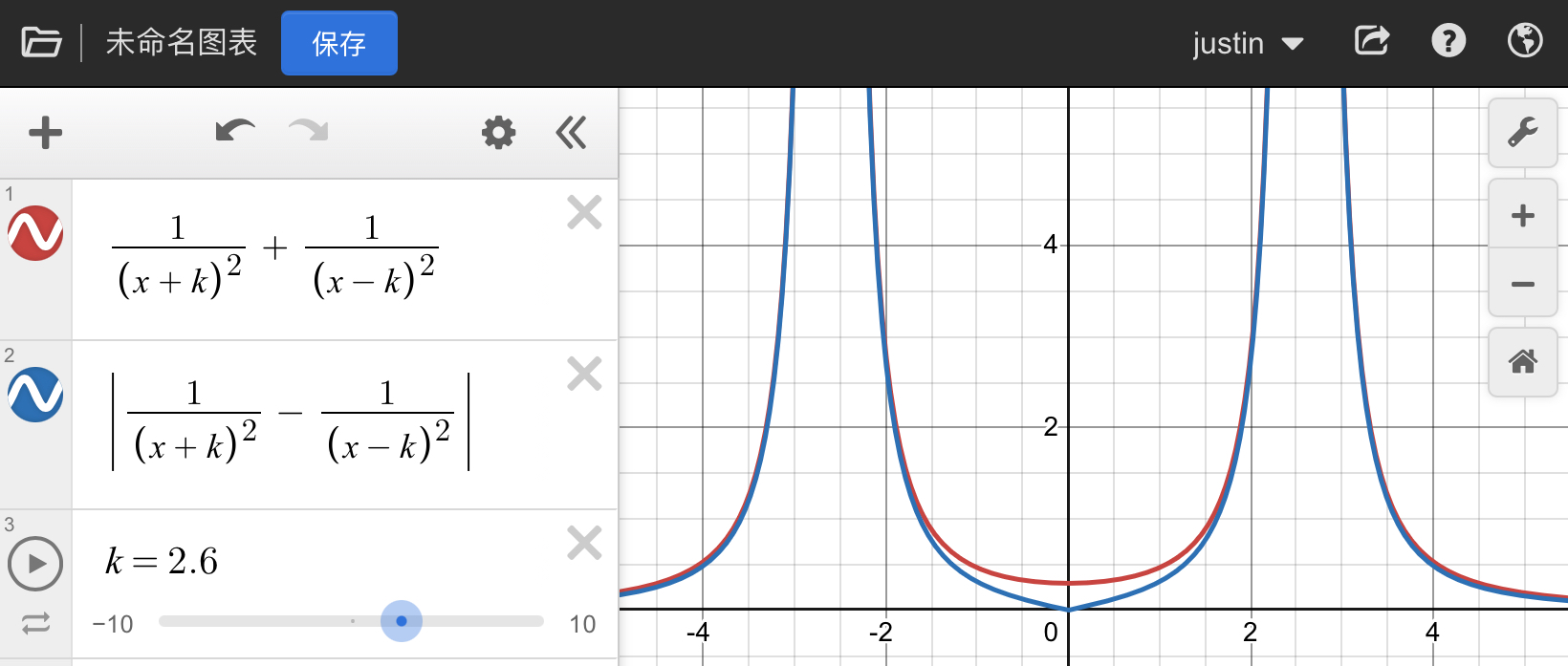
在两同种电荷连线的垂直平分线上，场强先变大后变小；对于异种电荷的情况，一直变小。
特殊地，如果电场中各点的电场强度的大小相等、方向相同，这个电场就叫作匀强电场。匀强电场的电场线可以用间隔相等的平行线来表示。相距很近的一对带等量异种电荷的平行金属板，它们之间的电场除边缘外，可以看作匀强电场。
静电的防止与利用
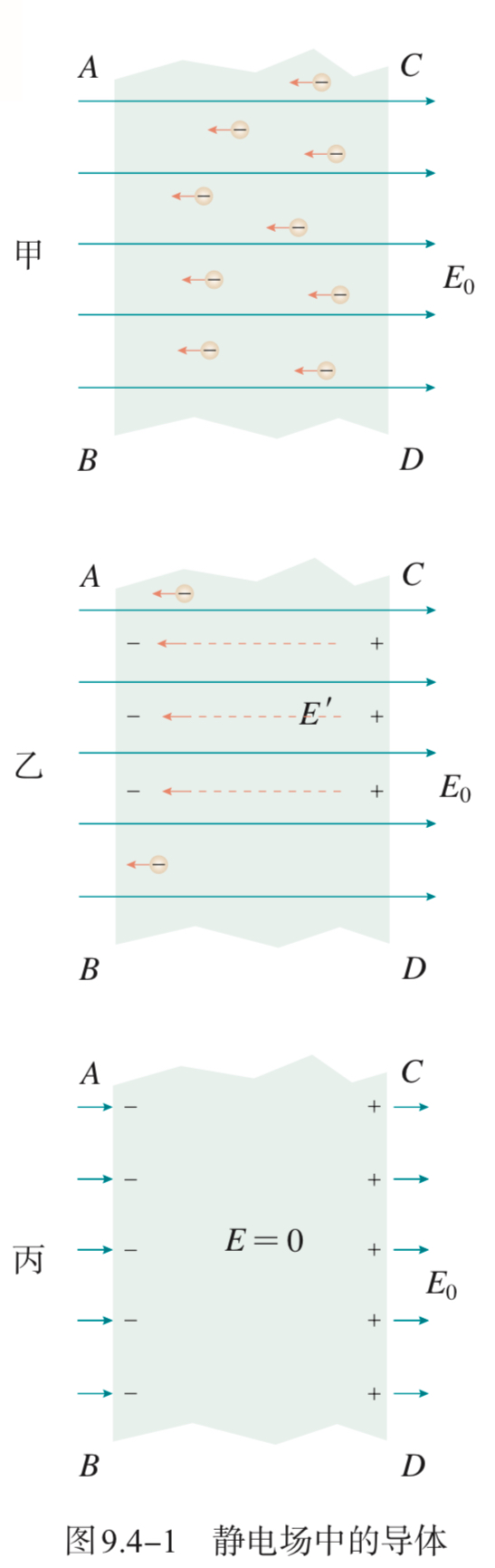
对于静电场中一不带电的导体，其中的自由电子在库仑力的作用下，向电场反方向运动（其实类似于感应起电），这也就导致导体中的电场变大，但是由于导体中的电场与外部静电场叠加仍然不等于零，故自由电子继续运动，直到叠加后电场等于零，我们也称此状态为静电平衡。
注意到处于静电平衡状态的导体电荷均分布于导体表面，则如果此导体空腔，那么腔内电场强度为零，即不受外电场干扰，这种技术被称为静电屏蔽。
由于处于静电平衡状态的导体电荷均分布于导体表面，且越尖锐的位置，电荷的密度（单位面积的电荷量）越大，周围的电场强度越大，这种强电场使得空气分子中的正负电荷分离，即空气的电离。电离所得的带正/负粒子被电场加速从而电离更多分子。
那些所带电荷与导体尖端的电荷符号相反的粒子，由于被吸引而奔向尖端，与尖端上的电荷中和，这相当于导体从尖端失去电荷。这种现象叫作尖端放电。
避雷针通过接地，获得源源不断的电荷，从而中和空气中的电荷。
在电场中，带电粒子受到静电力的作用，向着电极运动，最后会被吸附在电极上。这一原理在生产技术上被广泛应用。
发表回复