AI Summary
本文介绍了Linux系统中load平均的计算原理,包括任务状态分类、指数移动平均(EMA)算法的推导与实现,以及其在系统负载降噪中的应用。通过详细解读内核源码和数学公式,帮助读者理解load的统计机制与更新方式。
引言
话说这几天服务器一直不太稳定,uptimerobot的警报响个不停,但是每次等我看到警报,要么已经好了,要么直接就登不上去了,十分气人。
非常巧的是,就在昨天,我又收到了警报,还成功登上了服务器!我一看,为什么CPU十分悠闲(只有不到 5% 的利用率),但与此同时Load average已经飙升到 16.75 了呢?换句话说,Load不止于CPU有关,那么它是如何计算的呢?

了解相关因素
(希望学习数学的同学请空降下一段)
查阅资料我们得知,system load实际上只与 rq 中所有 “active” 的任务数 有关。
rq (runqueue) 表示 CPU 上的运行队列,而“active”的任务包括:
- TASK_RUNNING
这个任务正在某个 CPU 上运行(运行,RUNNING)
这个任务正在等待 CPU(就绪,READY),即进程申请到了CPU以外的其它全部资源,只要有 CPU 空出来就能跑。
- TASK_UNINTERRUPTIBLE
指不可中断睡眠,表示任务在等待某些内核资源,即使收到信号也要等到内核资源调用完毕后再结束(例如 kill -9 发出的 SIGKILL ),这样的状态包括等待内存页调入、等待网络or磁盘 I/O,比如你正在读取/写入一个大文件,此时怎么 kill 也 kill 不掉,这样设计是为了避免在关键资源访问时被打断,导致内核数据结构不一致。
问题就来了,I/O 阻塞的任务其实没占 CPU,而READY的任务其实也没有,load为什么要数它们呢?
实际上,load average 衡量的是系统的调度压力,也就是有多少task要被运行,类似于明天就要报道了,你还有多少作业需要做 😉
言归正传,我们执行 sudo iostat -o,便可以看到…
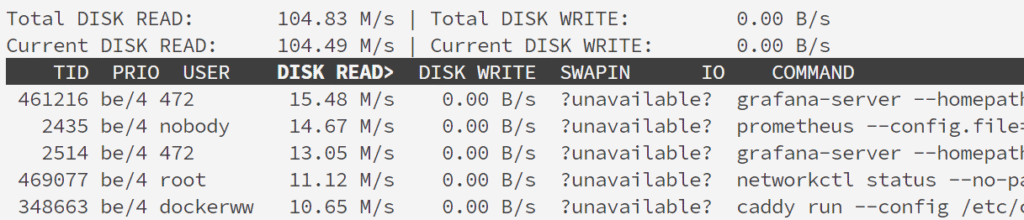
果然是这样的!(我挂载的云盘最高允许READ是150M/s,所以104M/s已经是相当高了)
小知识,TASK_INTERRUPTIBLE 是指可中断睡眠,与 TASK_UNINTERRUPTIBLE 不同,这样的等待不涉及内核,因而允许直接被 kill 掉,常见的包括等待socket、sleep。
了解更新方式
我们已经了解了load与什么有关,那么我们在头图中的三个load(1min,5min,15min)分别是如何计算出来的呢?
不装了,直接上 linux/include/linux/sched/loadavg.h · torvalds/linux。
分数处理
首先,为了保证内核的运行效率,开发者在内核中全部使用整数而非浮点数,load也不例外,因而有
/*
* These are the constant used to fake the fixed-point load-average
* counting. Some notes:
* - 11 bit fractions expand to 22 bits by the multiplies: this gives
* a load-average precision of 10 bits integer + 11 bits fractional
* ...
*/
extern unsigned long avenrun[]; /* Load averages */
#define FSHIFT 11 /* nr of bits of precision */
#define FIXED_1 (1<<FSHIFT) /* 1.0 as fixed-point */
#define LOAD_FREQ (5*HZ+1) /* 5 sec intervals */
#define LOAD_INT(x) ((x) >> FSHIFT)
#define LOAD_FRAC(x) LOAD_INT(((x) & (FIXED_1-1)) * 100)在这里,开发者将后10位都留给小数,即第11位开始表示整数部分,因此 FIXED_1 才代表1,而 LOAD_INT 加载整数部分,LOAD_FRAC 加载两位小数。
指数移动
/*
* ...
* - if you want to count load-averages more often, you need more
* precision, or rounding will get you. With 2-second counting freq,
* the EXP_n values would be 1981, 2034 and 2043 if still using only
* 11 bit fractions.
*/
#define LOAD_FREQ (5*HZ+1) /* 5 sec intervals */
static inline unsigned long
calc_load(unsigned long load, unsigned long exp, unsigned long active){
// ...
}终于开始真正计算了!LOAD_FREQ 即为采样周期,在这里是5秒钟(常量 HZ 是指 每秒触发的硬件定时器中断,类似于一个每秒会触发 HZ 次的定时器),calc_load 就用来计算load的。
正如上一节提到过的,作为内核,效率是第一位的。“15分钟”的load,内核不愿意将 $15 \times 60 \div 5=180$ 个时刻的active都保留下来参与运算,我们需要一种高效的方式表示一段时间内active的趋势。
”一段时间“,这启示我们可以考虑取(未加权)平均数,这就是简单移动平均(SMA)。它其实不太高效,考虑当前有 $\bar {x}_{prev}={\frac {\sum_{i=1}^{n}x_{i}}{n}}={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}$, 我们则有 $\overline{p} = \overline{p}_{prev} + \frac{1}{n} (p_M – p_{M-n}).$,这依然要求我们保存前15分钟的值。
而且这种方法不能够反应最近的数据,加权平均数可以解决这个问题,但是它更新没有简便的方法(太耗时)。我们有指数移动平均(英语:exponential moving average,EMA或EWMA):
$$S_{t} = \alpha \times Y_{t} +(1-\alpha) \times S_{t-1}$$
将 $S_{t-1}$ 带入 $S_t$,再带 $S{t-2}$…可得
$$S_{t} = \alpha \times ( p_{t} +(1-\alpha)p_{t-1} +(1-\alpha)^2 p_{t-2} +(1-\alpha)^3 p_{t-3} + \cdots)$$
也就是说,$p_x$ 获得 $(1-\alpha)^{t-x}\times \alpha$ 的权重,这恰好满足了”反应最近的数据“的要求,而由于越远权值越小,我们得以通过调整 $\alpha$ 调整”最远记忆到哪里“,具体地,system load里的”1min”指的是1分钟之前的数据取得权重 $\frac{1}{e}\doteq 0.36$ 的EMA,下面我们从 $e$ 的定义式开始,推出 $\alpha$ 的取值:
我们要求 “在时间差 T(比如 1 分钟)时,权重衰减到 1/e”,那写出方程。
$$(1-\alpha)^k = \frac{1}{e},\qquad k=\frac{T}{\Delta t}.$$
两边取对数,得
$$k\ln(1-\alpha) = -1 \quad\Rightarrow\quad \ln(1-\alpha) = -\frac{1}{k}.$$
于是
$$1-\alpha = e^{-1/k} \quad\Rightarrow\quad \boxed{\alpha = 1 – e^{-1/k}}.$$
把 $k=T/\Delta t$ 代回:
$$\boxed{\alpha = 1 – e^{-\Delta t / T}}.$$
推导过程由ChatGPT启发,https://chatgpt.com/s/t_68b307cd4c3881918bcf22278739250e
#define EXP_1 1884 /* 1/exp(5sec/1min) as fixed-point */
#define EXP_5 2014 /* 1/exp(5sec/5min) */
#define EXP_15 2037 /* 1/exp(5sec/15min) */
/*
* a1 = a0 * e + a * (1 - e)
*/
static inline unsigned long
calc_load(unsigned long load, unsigned long exp, unsigned long active)
{
unsigned long newload;
newload = load * exp + active * (FIXED_1 - exp);
if (active >= load)
newload += FIXED_1-1;
return newload / FIXED_1;
}让我们带入1min,和内核中预定义的常量对比验算一下:
所谓 EXP_1 实则是 $1-\alpha$,因为它作为参数 exp 被传入后,与 load 相乘了。则根据上方公式,
$$
\alpha= e^{-\Delta t / T}=e^{-5/60}\doteq1884.25096
$$
这里有更多信息:Exponential smoothing – Wikipedia。坏消息,没有中文。
实际运用
说了这么多,这玩意有什么(除了Linux的System Load)用呢?
有的,我们可以用它来降噪!
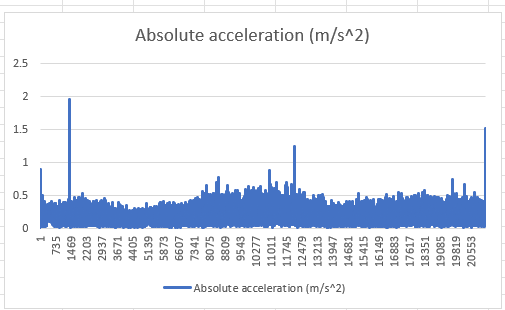
下面是一个我用phyphox收集的加速度数据,数据波动还是十分大,用来分析极为不方便,可以考虑采用EMA降噪。限于篇幅,请读者自行尝试。
发表回复