趣题巧解

昨晚碰到一个很有意思的数学题，并且十分罕见地做了出来。代数能力不错的朋友可以挑战一下。

$$ a, b, c满足 a=ab+c; b=bc+a; c=ca+b$$

要求这三个数的和 $a+b+c$ .

暂停0.47223924秒进行思考。

先注意到a=b=c=0为一组解，此时a+b+c=0;

再注意到:

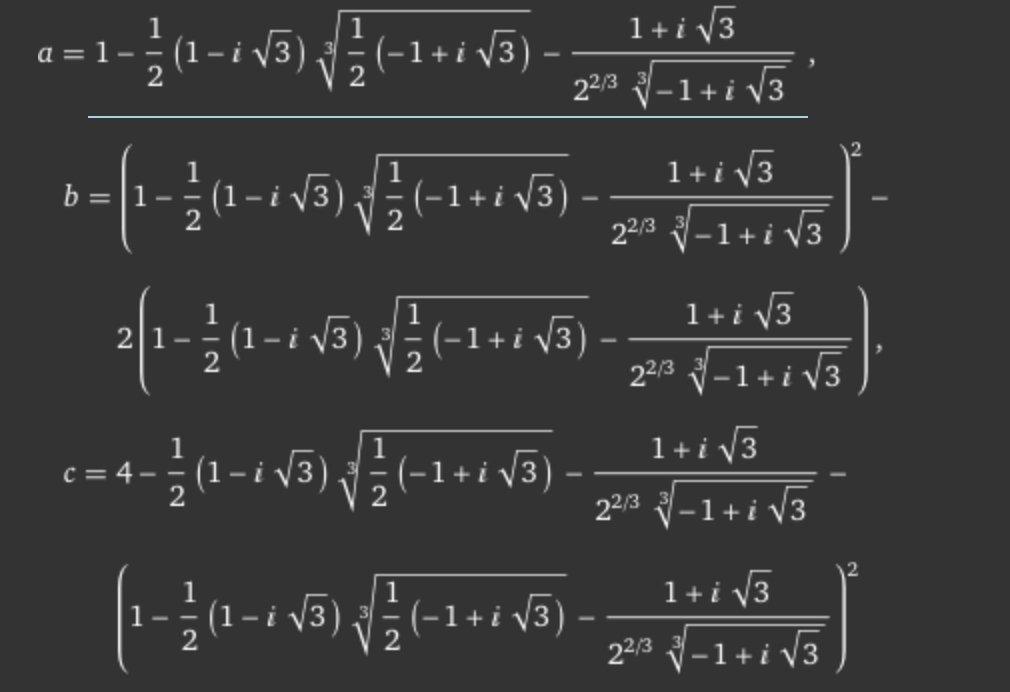
为第二组解（剩下两组a, b, c交换位置即可）

暂停0.22474239计算a+b+c的值。

接下来分享人类做法：

但凡有点数学基础，都会先把三式相加两边消去a+b+c得到ab+bc+ca=0

此时此刻如果你有奚望智商的十分之一，你会去想什么情况下能出现ab+bc+ca?

$$(a+b+c)^2!$$

所以$$(a+b+c)^2=a^2+b^2+c^2+2\times0=a^2+b^2+c^2$$

所以要求a+b+c,求他们的平方和即可！

接下来的两步很有艺术性。

我们先分析三式找不同和相同点：相同点：不齐次；不同点：没有共同项，什么都合并不了！！！

这两点让人都极为苦恼，因为齐次可以瞎设（我超喜欢设的），而合并嘛，谁不喜欢合并小情侣？

于是我们着手处理这两个问题。

先看共同项，每个式子右边的乘积看上去离abc只有一字之差，所以我们两边同乘：

$$ac=abc+c^2$$ $$ ab=abc+a^2$$ $$ bc=abc+b^2 $$

太巧了！太妙了！既有ab+bc+ca这个已知量，又有共同项abc, 甚至还有要求量平方和！三式直接相加：

$$ac+bc+ca=a^2+b^2+c^2+3abc $$ $$a^2+b^2+c^2=-3abc $$

接下来处理不齐次：

这个二次项ab和一次项c鬼混，左边的a很不爽，于是把c给拉了过来再平方，这样子可以使左右两边分别“齐次”。

$$ a^2-2ac+c^2=a^2 b^2 $$ $$ b^2-2ba+a^2=b^2 c^2$$ $$ c^2-2bc+b^2=a^2 c^2 $$

你看到了吧。你看到了吗？你看到了！三式相加：

$$ 2(a^2+b^2+c^2)-2\times(ac+bc+ca)=a^2b^2+b^2c^2+c^2a^2 $$

右边看上去挺唬人，但每一项都是平方，所以可以推测出$$ RHS=(ab+bc+ca)^2-2abc(a+b+c)$$会很有用。

$$ a^2+b^2+c^2=-abc(a+b+c)$$

太妙了！太巧了！左边即要求的a+b+c（下设为x,因为他善）的平方，右边的-abc正好与$$ x^2$$有关。

$$ x^2=\frac{x^2}{3} x$$ $$ 1=\frac{x}{3}$$

所以a+b+c=x=3!

综上，a+b+c=3或0

Notes:小说明后天更